Elm で作る TaPL のラムダ計算(その2)
本記事は「言語実装 Advent Calendar 2019」の7日目の記事です.
表題の通り,TaPL という書籍で紹介されているプログラミング言語の実装例を Elm でやってみたという話です(その2). その1はこちら.
- 第4章 算術式のML実装
- 第7章 ラムダ計算の ML 実装 (本記事はココ)
- 型無しラムダ計算を実装
- 以降はこれを拡張していく(たしか)
- 第10章 単純型のML実装
- 7章のを型付きラムダ計算にする
- 第17章 部分型付けの ML 実装
- 第25章 System F の ML 実装
- 最後に型の多相性を追加
実装は全て下記のリポジトリにあげています:
また,前回同様にWeb ブラウザから遊べるようになってます.
第7章 ラムダ計算の ML 実装
さぁいよいよみんな大好き(型なし)ラムダ計算です. ちなみに,ラムダ計算の数理論理学的な議論は5章でしている.
構文規則
構文規則はこんな感じ:
t := x [変数]
| \x . t [ラムダ抽象]
| t t [関数適用]
v := \x . tなんと前回の算術式より構文規則がシンプル. ラムダ計算というのは「関数」しかないプログラミング言語で,ラムダ抽象というのが最近の多くの言語で導入されている無名関数や関数オブジェクトと言われるものだ(たぶん).
まずはこれを Elm 上の型として定義する:
type Term
= TmVar Int Int
| TmAbs String Term
| TmApp Term Term
-- 値はラムダ抽象だけ
isval : Context -> Term -> Bool
isval _ t =
case t of
TmAbs _ _ ->
True
_ ->
False
-- 変数名を保持している(表示用)
-- Binding の意味は現状まだない(次回以降ちゃんと使う)
type alias Context = List ( String, Binding )
type Binding = NameBindTmVar が少しキモ. 2つの Int は変数が関数全体の中でどの位置にいるかを表している:
- 1つ目の Int はドブラウン・インデックス (束縛されたラムダ抽象までの距離)
- 2つ目の Int は一番外のラムダ抽象までの距離(深さ)
- e.g.
(\x. \f. f x) (\x. x)の場合はTmApp (TmAbs "x" (TmAbs "f" (TmApp (TmVar 0 2) (TmVar 1 2)))) (TmAbs "x" (TmVar 0 1))
ちなみに,TmAbs String Term の文字列型は変数名で基本的に表示用.
評価規則
評価規則も同様にシンプル:
t1 => t1'
---------------
t1 t2 => t1' t2
t2 => t2'
---------------
v1 t2 => v1 t2'
(\x.t12) v2 -> [x|-> v2]t123つ目のが関数適用で,[x|-> v2]t12 記法は t12 内の変数 x を全て v2 に置き換えるという意味である. ここで,v2 が値というのがキモだ. すなわち正格評価される.
これをパターンマッチを使って実装すると次の通り:
-- 止まらない可能性があるから注意
eval : Context -> Term -> Maybe Term
eval ctx t =
if isval ctx t then
Just t
else
Maybe.andThen (eval ctx) (eval1 ctx t)
eval1 : Context -> Term -> Maybe Term
eval1 ctx t =
case t of
TmApp (TmAbs x t12) t2 ->
if isval ctx t2 then
Just (termSubstTop t2 t12)
else
Maybe.map (TmApp (TmAbs x t12)) (eval1 ctx t2)
TmApp t1 t2 ->
Maybe.map (flip TmApp t2) (eval1 ctx t1)
_ ->
Nothing
termSubstTop : Term -> Term -> Term
termSubstTop = ...termSubstTop という新しい関数が出てきた. 変数を置き換える(代入する)上で重要なのは同じ変数名の変数が出てきたときに,それらを区別して〜〜ってのがあり,それをいい感じにやるための工夫が TmVar の2つの Int だ. この実装上の工夫は第6章で説明されているので,買って読んでください(おい).
で,termSubstTop の実装はこんな感じ(本書にも全部書いてある):
-- v2 と t12 を渡して [x|->v2]t12 が返ってくる
-- termSubst 0 なので一番外の変数を置き換える
-- 置き換えた後 -1 シフトしないといけない(一番外のラムダ抽象が剥がれるので)
-- 先に 1 だけシフトしてるのは代入後の s は -1 シフトして欲しくないから
termSubstTop : Term -> Term -> Term
termSubstTop s t =
termShift -1 (termSubst 0 (termShift 1 s) t)
-- 項 tt 中の j 番の変数へ項 s を代入 [j|->s]t する
termSubst : Int -> Term -> Term -> Term
termSubst j s tt =
let
walk c t =
case t of
TmVar x n ->
if x == j + c then
-- 潜ったぶんだけドブラウン・インデックスをシフト
termShift c s
else
TmVar x n
TmAbs x t1 ->
TmAbs x (walk (c + 1) t1)
TmApp t1 t2 ->
TmApp (walk c t1) (walk c t2)
in
walk 0 tt
-- 項 tt の自由変数のドブラウン・インデックスを d だけシフト
termShift : Int -> Term -> Term
termShift d tt =
let
walk c t =
case t of
TmVar x n ->
-- c はラムダ抽象の深さ
-- x は変数が束縛されたのラムダ抽象までの距離
-- したがって x >= c は自由変数
if x >= c then
TmVar (x + d) (n + d)
else
TmVar x (n + d)
TmAbs x t1 ->
TmAbs x (walk (c + 1) t1)
TmApp t1 t2 ->
TmApp (walk c t1) (walk c t2)
in
walk 0 ttREPL で確かめてみる:
$ elm repl
---- Elm 0.19.1 ----------------------------------------------------------------
Say :help for help and :exit to exit! More at <https://elm-lang.org/0.19.1/repl>
--------------------------------------------------------------------------------
> import TaPL.Chap7 as Chap7 exposing (Term (..))
> Chap7.eval [] (TmApp (TmAbs "x" (TmAbs "f" (TmApp (TmVar 0 2) (TmVar 1 2)))) (TmAbs "x" (TmVar 0 1)))
Just (TmAbs "f" (TmApp (TmVar 0 1) (TmAbs "x" (TmVar 0 2))))
: Maybe Term(\x . (\f . f x)) (\x . x) を評価して \f . f (\x . x) という結果を得た.
文字列へ変換
変数がインデックス表記になっているため読みにくい. なので文字列への変換関数とパーサーを記述しよう.
まずは文字列の変換から. こっちは TaPL にも(ほとんど)書いてある:
-- これは TaPL にはない
display : Term -> String
display t =
printtm [] t
|> Maybe.map (dropIfStartsWith "(") -- 最初と最後のカッコを消している
|> Maybe.map (dropIfEndsWith ")")
|> Maybe.withDefault ""
-- インデックスが間違っている場合は Nothing になる
printtm : Context -> Term -> Maybe String
printtm ctx t = ...前回と異なり,今回は文字列に変換できない場合がある. インデックスが間違っている場合だ. その場合は Notihng が返るようにしている(TaPL の場合は例外). printtm は Term 型に対するパターンマッチで記述する:
printtm : Context -> Term -> Maybe String
printtm ctx t =
case t of
TmAbs x t1 ->
let
( ctx1, x1 ) =
-- 被らない変数名を生成
pickfreshname ctx x
in
Maybe.map
(\s1 -> String.concat [ "(\\", x1, ". ", s1, ")" ])
(printtm ctx1 t1)
TmApp t1 t2 ->
Maybe.map2
(\s1 s2 -> String.concat [ "(", s1, " ", s2, ")" ])
(printtm ctx t1)
(printtm ctx t2)
TmVar x n ->
-- ctx には変数がどんどん保存される
-- そのため ctx の長さと n の長さが等しくないといけない
if ctxlength ctx == n then
-- ctx から変数名をドブラウン・インデックスで引いてくる
index2name ctx x
else
Nothingpickfreshname や ctxlength や index2name の実装は本書にはない. 振る舞いの説明が書いてあるので,それを読んで実装する必要がある. なので,僕は次のように実装したがもう少しエレガントな実装があるかもしれない:
-- 変数名が重複しないように後ろに ' を足して Context の先頭に追加
pickfreshname : Context -> String -> ( Context, String )
pickfreshname ctx x =
let
x1 =
ctx
|> List.map Tuple.first
|> List.filter (String.startsWith x)
|> List.maximum
|> Maybe.map (\a -> a ++ "'")
|> Maybe.withDefault x
in
( ( x1, NameBind ) :: ctx, x1 )
ctxlength : Context -> Int
ctxlength ctx =
List.length ctx
-- ドブラウン・インデックスは束縛されたラムダ抽象への距離
-- Context はラムダ抽象のたびに先頭に対応する変数を追加する
-- なので,そのままリストへのインデックスアクセスで良い
index2name : Context -> Int -> Maybe String
index2name ctx x =
case List.getAt x ctx of
Just ( str, _ ) ->
Just str
_ ->
NothingREPL で試してみよう:
> Chap7.display (TmApp (TmAbs "x" (TmAbs "f" (TmApp (TmVar 0 2) (TmVar 1 2)))) (TmAbs "x" (TmVar 0 1)))
"(\\x. (\\f. (f x))) (\\x. x)" : String
> Chap7.eval [] (TmApp (TmAbs "x" (TmAbs "f" (TmApp (TmVar 0 2) (TmVar 1 2)))) (TmAbs "x" (TmVar 0 1))) |> Maybe.map Chap7.display
Just ("\\f. (f (\\x. x))") : Maybe Stringいい感じ.
パーサー
前回同様 elm/parser を使う. ドブラウン・インデックスなどを構築していく必要があるので,それらを保持した Context という型を用意する(紛らわしいが,モジュールが違い外に出さない型なので大丈夫):
module TaPL.Chap7.Parser exposing (parse)
import Parser exposing ((|.), (|=), Parser)
type alias Context =
{ env : Dict String Int -- 変数名とドブラウンインデックスの対応
, depth : Int -- ラムダ抽象の深さ
}
iniCtx : Context
iniCtx =
{ env = Dict.empty, depth = 0 }
parse : String -> Result (List Parser.DeadEnd) Term
parse =
Parser.run parser
parser : Parser Term
parser =
termParser iniCtx |. Parser.end
termParser : Context -> Parser Term
termParser ctx = ...まずは関数適用を無視してパーサーを定義する(難しいので):
termParser : Context -> Parser Term
termParser ctx =
-- oneOf は最初にマッチしたパース結果を採用する
Parser.oneOf
[ parParser ctx -- カッコのパーサー(割愛)
, absParser ctx
, varParser ctx
]
-- ラムダ抽象(`\x. t`)のパーサー
absParser : Context -> Parser Term
absParser ctx =
Parser.succeed identity
|. Parser.symbol "\\"
|. Parser.spaces
|= varStrParser
|. Parser.spaces
|. Parser.symbol "."
|. Parser.spaces
|> Parser.andThen (absParserN ctx)
-- 変数名のパーサー (小文字始まりで [A-z0-9_'] だけ許容する)
varStrParser : Parser String
varStrParser =
Parser.variable
{ start = Char.isLower
, inner = \c -> Char.isAlphaNum c || c == '_' || c == '\''
, reserved = Set.fromList []
}
-- ラムダ抽象が深くなるのでコンテキストを更新して再度 Term をパースする
absParserN : Context -> String -> Parser Term
absParserN ctx v =
Parser.succeed (TmAbs v)
|= Parser.lazy (\_ -> termParser <| pushVar v <| incrCtx ctx)
-- ラムダ抽象が1つ深くなる
-- なので深さと全てのドブラウン・インデックスを +1 する
incrCtx : Context -> Context
incrCtx ctx =
{ ctx | depth = ctx.depth + 1, env = Dict.map (\_ v -> v + 1) ctx.env }
-- 新しい変数名を追加する
-- 同じ変数名は上書きしてしまって良い
pushVar : String -> Context -> Context
pushVar v ctx =
{ ctx | env = Dict.insert v 0 ctx.env }
-- 変数のパーサー
varParser : Context -> Parser Term
varParser ctx =
varStrParser
|> Parser.andThen (lookupVar ctx)
|> Parser.map (flip TmVar ctx.depth)
-- コンテキストには変数名とドブラウン・インデックスの連想配列がある
-- なので,変数名で引っ張ってくるだけ
lookupVar : Context -> String -> Parser Int
lookupVar ctx s =
Dict.get s ctx.env
|> Maybe.map Parser.succeed
|> Maybe.withDefault (Parser.problem ("undefined variable: " ++ s))REPL で試してみる:
> import TaPL.Chap7.Parser as Parser
> Parser.parse "\\x. x"
Ok (TmAbs "x" (TmVar 0 1))
: Result (List Parser.DeadEnd) Term
> Parser.parse "\\x. (\\y . x)"
Ok (TmAbs "x" (TmAbs "y" (TmVar 1 2)))
: Result (List Parser.DeadEnd) Term
> Parser.parse "\\x. (\\y . z)"
Err [{ col = 12, problem = Problem ("undefined variable: z"), row = 1 }]
: Result (List Parser.DeadEnd) Term自由変数が出てくるとちゃんとエラーになる.
残るは関数適用だ. 実はこいつが難しい. というのも,雑に実装をするといわゆる左再帰が出てくるからだ.
なので,一工夫する必要がある:
termParser : Context -> Parser Term
termParser ctx =
-- 関数適用は t1 t2 なのでまずは t1 にマッチさせ
Parser.oneOf
[ parParser ctx
, absParser ctx
, varParser ctx
] -- 後から t2 を探す
|> Parser.andThen (appParser ctx)
-- 関数適用 t1 t2 のパーサー
appParser : Context -> Term -> Parser Term
appParser ctx t =
Parser.oneOf
[ Parser.succeed (TmApp t)
-- backtrackable や commit は一旦無視して良い
-- termWithoutAppParser が先に出てくるのは関数適用が左結合のため
-- 例: t1 t2 t3 は (t1 t2) t3 つまり (TmApp (TmApp t1 t2) t3)
|. Parser.backtrackable (Parser.symbol " " |. Parser.spaces)
|= Parser.lazy (\_ -> termWithoutAppParser ctx)
|> Parser.andThen Parser.commit
|> Parser.andThen (appParser ctx)
-- t2 がなければ t1 のまんま返す
, Parser.succeed t
]
-- 関数適用を抜いた termParser
termWithoutAppParser : Context -> Parser Term
termWithoutAppParser ctx =
Parser.oneOf
[ parParser ctx
, absParser ctx
, varParser ctx
]backtrackable と commit はパーサーが文字列を消費してしまう問題の解決方法だ. パーサーの処理が進むと対象の文字列をどんどん消費していく. oneOf で複数のパーサーを許容するとき,1文字目の結果で分岐できることが保証されているなら問題ないが,途中まで進み文字列を消費して失敗すると,その文字列を消費した状態で oneOf 内の次のパーサーへ進んでしまう. そこで,elm/parser の場合は消費を戻して欲しい場合はし backtrackable を使い,もう戻らなくて良くなった時点で commit を使う,という感じ(たぶん). まぁ今回は必要ではない気がするが,後々必要になってくる.
さぁ REPL で確認してみよう:
> Parser.parse "(\\x . \\f . f x) (\\x . x) (\\x . (\\x . x))"
| |> Result.toMaybe
| |> Maybe.andThen (Chap7.eval [])
| |> Maybe.map Chap7.display
|
Just ("\\x. x") : Maybe String完璧だ.
おまけ: SPA にする
今回も同様に SPA にする. 章ごとにページ分けても良かったが,試しに一つにまとめてみた. つまり,4章の言語と7章の言語を同じように扱う. どちらも:
- 文字列をパースする(
parse) - 項を1ステップ評価する(
eval1) - 項を文字列に変換する(
display)
をしたい. こういった場合,多くの言語ではインターフェースや型クラスのようなアドホック多相を利用する. しかし,Elm にはアドホック多相はない. そのため,パラメトリック多相で模倣する:
-- 各章の言語の Context と Term 型を受け取る
type alias Calculus ctx t =
{ parse : String -> Result (List Parser.DeadEnd) t
, eval1 : ctx -> t -> Maybe t
, display : t -> String
, init : ctx -- Context の初期値
, logs : List t -- Term の履歴(表示用)
}
parse : String -> Calculus ctx t ty -> Result (List Parser.DeadEnd) (Calculus ctx t ty)
eval1 : Calculus ctx t ty -> Maybe (Calculus ctx t ty)
display : Calculus ctx t ty -> List StringCalculus には章ごとに型が異なるものを全部突っ込む必要がある. そのため logs のようなフィールドもある(前回 Model 型の exps にあったやつ). この型の値を各章ごとに定義しよう:
type Chapter
= Chap0
| Chap4 (Calculus () Chap4.Term)
| Chap7 (Calculus Chap7.Context Chap7.Term)
init : String -> Chapter
init s =
case s of
"chap4" ->
Chap4
{ parse = Chap4.parse
, eval1 = \_ -> Chap4.eval1
, display = Chap4.display
, init = ()
, logs = []
}
"chap7" ->
Chap7
{ parse = Chap7.parse
, eval1 = Chap7.eval1
, display = Chap7.display
, init = []
, logs = []
}
parse : Chapter -> String -> Result (List Parser.DeadEnd) Chapter
eval1 : Chapter -> Maybe Chapter
display : Chapter -> List Stringあとは Chapter 型を main の Model に持たせて,それぞれの関数を Chapter のものへと置き換えるだけ. これが良い方法かどうか,正直なんとも言えないが面白いモノができたの個人的には満足.
おしまい
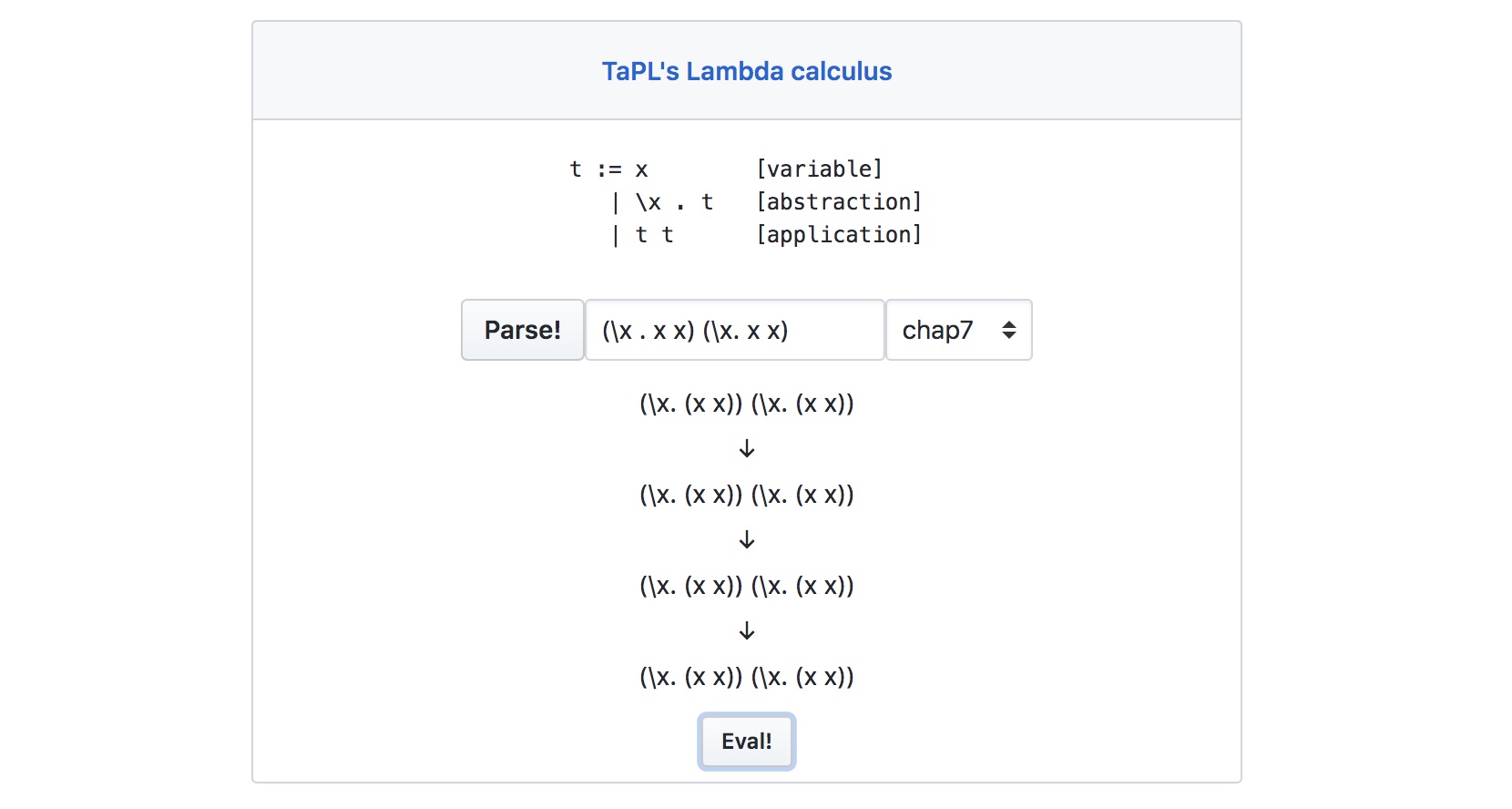
ところで,型なしラムダ計算は停止しない場合がある(例えば (\x . x x) (\x . x x) とか). このような式を SPA に突っ込むと無限に eval ボタンを押せてしまう. そこで,同期からは「eval ボタンが下にずれていくから無限プチプチみたいなのができない」と言われた笑. 検討した結果,ボタン固定にすると式の結果を追うのに上下スクロールを何回もしないとなので却下した(ごめんね).