Elm で作る TaPL のラムダ計算(その3)
本記事は「IGGG Advent Calendar 2019」の10日目の記事です.
表題の通り,TaPL という書籍で紹介されているプログラミング言語の実装例を Elm でやってみたという話です(その3). その1とその2はこちら.
- 第4章 算術式のML実装
- 第7章 ラムダ計算の ML 実装
- 第10章 単純型のML実装 (本記事はココ)
- 7章のを型付きラムダ計算にする
- 第17章 部分型付けの ML 実装
- 第25章 System F の ML 実装
- 最後に型の多相性を追加
実装は全て下記のリポジトリにあげています:
また,今まで同様にWeb ブラウザから遊べるようになってます.
第10章 単純型の ML 実装
さて,いよいよみんな大好き「型」の登場だ. 10章は少し面白くて,4章で実装した算術式の真偽値に関する部分と7章の型なしラムダ計算を組み合わせて,更にそれに型をのせるプログラミング言語を実装する. つまり,今までの実装をちゃんとやっていれば割とサクッとできています.
なお,同期各位は全然やらなかったせいか10章を5週ぐらいやっている笑.
構文規則
t := x [変数]
| \x:T.t [ラムダ抽象]
| t t [関数適用]
| true
| false
| if t then t else t
v := \x:T.t
| true
| false
T := Bool [真偽値型]
| T -> T [関数型]ラムダ抽象には型注釈(:T の部分)がある. なんで付けるのかとかは9章に書いてあるのでぜひ TaPL を買って読んでください(おい). これを Elm の型として実装する:
type Term
= TmVar Int Int
| TmAbs String Ty Term
| TmApp Term Term
| TmTrue
| TmFalse
| TmIf Term Term Term
type Ty
= TyArr Ty Ty -- Arrow の Arr ね
| TyBool
isval : Context -> Term -> Bool
isval _ t =
case t of
TmAbs _ _ _ ->
True
TmTrue ->
True
TmFalse ->
True
_ ->
False
type alias Context = List ( String, Binding )
type Binding = NameBind型の型 Ty 以外は,4章と7章の Term や isval を合体させているだけだ.
評価規則
// 7章の評価規則
t1 => t1'
---------------
t1 t2 => t1' t2
t2 => t2'
---------------
v1 t2 => v1 t2'
(\x:T.t12) v2 -> [x|-> v2]t12
// 4章の評価規則
if true then t2 else t3 => t2
if false then t2 else t3 => t3
t1 -> t1'
-------------------------------------------------
if t1 then t2 else t3 => if t1' then t2 else t3評価規則も同様に型注釈の構文が追加されただけでほとんど変わらない. 変わらないということはすなわち,実行時(評価)には型の有無は影響しないということだ. 構文規則同様,4章と7章の実装を組み合わせることで実装が終わる:
eval : Context -> Term -> Maybe Term
eval ctx t =
if isval ctx t then
Just t
else
Maybe.andThen (eval ctx) (eval1 ctx t)
-- あらゆる TmAbs のパターンマッチに Ty のパラメーターを追加する必要はある
eval1 : Context -> Term -> Maybe Term
eval1 ctx t =
case t of
TmApp (TmAbs x ty t12) t2 ->
if isval ctx t2 then
Just (termSubstTop t2 t12)
else
Maybe.map (TmApp (TmAbs x ty t12)) (eval1 ctx t2)
TmApp t1 t2 ->
Maybe.map (flip TmApp t2) (eval1 ctx t1)
TmIf TmTrue t2 _ ->
Just t2
TmIf TmFalse _ t3 ->
Just t3
TmIf t1 t2 t3 ->
eval1 ctx t1 |> Maybe.map (\t1_ -> TmIf t1_ t2 t3)
_ ->
Nothing
-- t に s を代入する
termSubstTop : Term -> Term -> Term
termSubstTop s t = ...型付け規則
ここからが新しい. いわゆる型検査のことだ. TaPL では「正しく型付けされた項はおかしくならない」という性質(安全性・健全性ともいう)について議論されている(8章で). 例えば,これから定義する型検査が通った項(Term)は eval 関数を適用しても無限ループなどにはならない. さて,そのための型付け規則は次のようになっている:
// 真偽値の型付け規則
true : Bool
false : Bool
t1 : Bool t2 : T t3 : T
-------------------------------
if t1 then t2 else t3 : T
// 単純ラムダ計算の型付け規則
x : T ∈ Γ
-----------
Γ ⊢ x : T
Γ, x : T1 ⊢ t2 : T2
-----------------------------
Γ ⊢ \x : T1 . t2 : T1 -> T2
Γ ⊢ t1 : T11 -> T12 Γ ⊢ t2 : T11
-------------------------------------
Γ ⊢ t1 t2 : T12ここで新しく出てくる Γ は型環境と言い,変数と型の対応関係を線形リストのような感じに保持している. Γ ⊢ t : T というのは「型環境 Γ のもと項 t は型 T に型付け可能」という風に読める(たぶん). まぁ実装してみればわかる(ほんとか?):
-- 型環境には Context を再利用する
type alias Context = List ( String, Binding )
type Binding
= NameBind
| VarBind Ty -- 変数の型を保持
-- 項 t の型が最終的に導出できれば型付け可能ということになる
typeof : Context -> Term -> Maybe Ty
typeof ctx t =
case t of
TmVar x _ ->
-- Context から型情報を引っ張ってくる
getTypeFromContext ctx x
TmAbs x ty1 t2 ->
let
-- Context に 変数と型の対応を追加する
ctx1 = addbinding ctx x (VarBind ty1)
in
-- ラムダ抽象は中の項 t2 が型付け可能である必要がある
typeof ctx1 t2
|> Maybe.map (\ty2 -> TyArr ty1 ty2)
TmApp t1 t2 ->
case ( typeof ctx t1, typeof ctx t2 ) of
( Just (TyArr ty11 ty12), Just ty2 ) ->
-- 関数適用の場合は引数の型 ty11 と適用する項の型 ty2 が同じである必要がある
if ty11 == ty2 then
Just ty12
else
Nothing
_ ->
Nothing
TmTrue ->
Just TyBool
TmFalse ->
Just TyBool
TmIf t1 t2 t3 ->
case ( typeof ctx t1, typeof ctx t2, typeof ctx t3 ) of
( Just TyBool, Just ty2, Just ty3 ) ->
-- if-then-else の場合は t2 と t3 の型が同じである必要がある
if ty2 == ty3 then
Just ty2
else
Nothing
_ ->
Nothing
getTypeFromContext : Context -> Int -> Maybe Ty
getTypeFromContext ctx idx =
case getbinding ctx idx of
Just (VarBind ty) ->
Just ty
_ ->
Nothing
getbinding : Context -> Int -> Maybe Binding
getbinding ctx n =
case ( ctx, n ) of
( [], _ ) ->
Nothing
( ( _, bind ) :: _, 0 ) ->
Just bind
( _ :: next, _ ) ->
getbinding next (n - 1)
addbinding : Context -> String -> Binding -> Context
addbinding ctx x bind =
( x, bind ) :: ctxREPL で試してみる:
> import TaPL.Chap10 as Chap10 exposing (Term(..), Ty(..), Binding(..))
-- (\x : (Bool -> Bool) . (\f : (Bool -> Bool -> Bool) . f x)) (\x : Bool . x)
> Chap10.typeof [] (TmApp (TmAbs "x" (TyArr TyBool TyBool) (TmAbs "f" (TyArr (TyArr TyBool TyBool) TyBool) (TmApp (TmVar 0 2) (TmVar 1 2)))) (TmAbs "x" TyBool (TmVar 0 1)))
Just (TyArr (TyArr (TyArr TyBool TyBool) TyBool) TyBool)
: Maybe Ty
-- (\x . x x) (\x . x x) はうまく型付けできない
> Chap10.typeof [] (TmApp (TmAbs "x" (TyArr TyBool TyBool) (TmApp (TmVar 0 1) (TmVar 0 1))) (TmAbs "x" (TyArr TyBool TyBool) (TmApp (TmVar 0 1) (TmVar 0 1))))
Nothing : Maybe Ty文字列に変換
基本的に4・7章の定義を利用すれば良いのだが,型注釈ができるようになったので型も変換できるようにする:
display : Term -> String
display t =
printtm [] t
|> Maybe.map (dropIfStartsWith "(") -- 最初と最後のカッコを消している
|> Maybe.map (dropIfEndsWith ")")
|> Maybe.withDefault ""
printtm : Context -> Term -> Maybe String
printtm ctx t =
case t of
TmAbs x ty t1 ->
let -- 重複しない変数名を生成して Context に積む
( ctx1, x1 ) = pickfreshname ctx x
in
Maybe.map
(\s1 -> String.concat [ "(\\", x1, " : ", printty ty, ". ", s1, ")" ])
(printtm ctx1 t1)
... -- あとは同じ
printty : Ty -> String
printty ty =
case ty of
TyArr ty1 ty2 ->
String.concat [ "(", printty ty1, " -> ", printty ty2, ")" ]
TyBool ->
"Bool"
-- Context から重複する変数名を探し ' を追加する
pickfreshname : Context -> String -> ( Context, String )
pickfreshname ctx x = ...REPL で試す:
> Chap10.display (TmApp (TmAbs "x" (TyArr TyBool TyBool) (TmAbs "f" (TyArr (TyArr TyBool TyBool) TyBool) (TmApp (TmVar 0 2) (TmVar 1 2)))) (TmAbs "x" TyBool (TmVar 0 1)))
"(\\x : (Bool -> Bool). (\\f : ((Bool -> Bool) -> Bool). (f x))) (\\x : Bool. x)"
: Stringパーサー
これも同様に4・7章の実装を合わせるだけ:
module TaPL.Chap10.Parser exposing (parse)
import Parser exposing ((|.), (|=), Parser)
import TaPL.Chap10 exposing (Term(..), Ty(..))
type alias Context =
{ env : Dict String Int
, depth : Int
}
iniCtx : Context
iniCtx =
{ env = Dict.empty, depth = 0 }
parse : String -> Result (List Parser.DeadEnd) Term
parse =
Parser.run parser
parser : Parser Term
parser =
termParser iniCtx |. Parser.end
termParser : Context -> Parser Term
termParser ctx =
Parser.oneOf
[ parParser ctx -- 括弧のパーサー
, absParser ctx -- ラムダ抽象のパーサー
, valParser -- ture/false のパーサー
, ifParser ctx -- if-then-else のパーサー
, varParser ctx -- 変数のパーサー
] -- 関数適用のパーサーだけ分けてるのは左再帰対策(その2参照)
|> Parser.andThen (appParser ctx)言わずもがな,型注釈のパースをする必要があるので,absParser はその2のと若干異なる:
absParser : Context -> Parser Term
absParser ctx =
Parser.succeed Tuple.pair
|. Parser.symbol "\\"
|. Parser.spaces
|= Parser.lazy (\_ -> varStrParser)
|. Parser.spaces
|. Parser.symbol ":" -- ここから
|. Parser.spaces
|= Parser.lazy (\_ -> tyParser) -- ここまでが追加
|. Parser.spaces
|. Parser.symbol "."
|. Parser.spaces
|> Parser.andThen (absParserN ctx)
-- 型のパーサー
tyParser : Parser Ty
tyParser =
Parser.oneOf
[ value "Bool" TyBool
]
|. Parser.spaces
-- これも左再帰対策(その2参照)
|> Parser.andThen tyArrParser
-- 関数型のパーサー
-- 関数型 T->T は右結合(T->T->T は T->(T->T) となる)
tyArrParser : Ty -> Parser Ty
tyArrParser ty =
Parser.oneOf
[ Parser.succeed (TyArr ty)
|. Parser.keyword "->"
|. Parser.spaces
|= Parser.lazy (\_ -> tyParser)
, Parser.succeed ty
]REPL で試してみる:
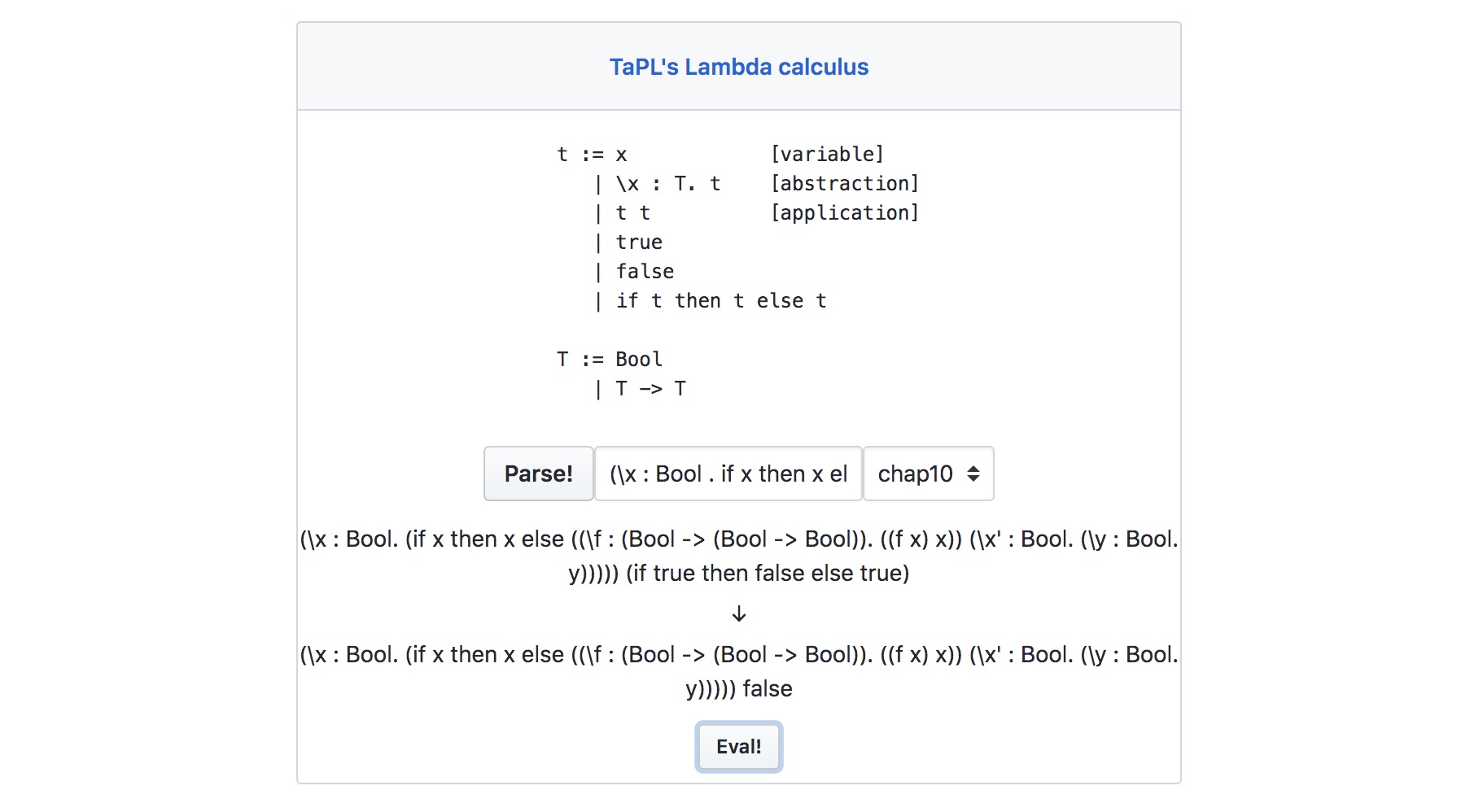
> "(\\x : Bool . if x then x else (\\f : Bool -> Bool -> Bool . f x x) (\\x : Bool . \\y : Bool . y)) (if true then false else true)"
| |> Parser.parse
| |> Result.toMaybe
| |> Maybe.andThen (\t -> Chap10.typeof [] t |> Maybe.map (always t)) -- 型検査
| |> Maybe.andThen (Chap10.eval [])
| |> Maybe.map Chap10.display
|
Just "false" : Maybe String完璧だ.
おまけ: SPA
前回整理したので基本的に足していくだけだ. ただし,型検査を Calculus に加える必要がある:
module TaPL.Calculus exposing (..)
type alias Calculus ctx t ty =
{ parse : String -> Result (List Parser.DeadEnd) t
, typeof : Maybe (ctx -> t -> Maybe ty) -- 追加
, eval1 : ctx -> t -> Maybe t
, display : t -> String
, init : ctx
, logs : List t
}
eval1 : Calculus ctx t ty -> Maybe (Calculus ctx t ty)
typecheck : Calculus ctx t ty -> Bool
parse : String -> Calculus ctx t ty -> Result (List Parser.DeadEnd) (Calculus ctx t ty)
display : Calculus ctx t ty -> List Stringあとは chap10 の定義も追加するだけ:
module TaPL exposing (..)
type Chapter
= Chap0
| Chap4 (Calculus () Chap4.Term Never)
| Chap7 (Calculus Chap7.Context Chap7.Term Never)
| Chap10 (Calculus Chap10.Context Chap10.Term Chap10.Ty)
init : String -> Chapter
init s =
case s of
"chap4" -> ...
"chap7" -> ...
-- 追加
"chap10" ->
Chap10
{ eval1 = Chap10.eval1
, display = Chap10.display
, parse = Chap10.parse
, init = []
, logs = []
, syntax = Chap10.syntax
, typeof = Just Chap10.typeof
}
_ ->
Chap0
parse : Chapter -> String -> Result (List Parser.DeadEnd) Chapter
eval1 : Chapter -> Maybe Chapter
typecheck : Chapter -> Bool
display : Chapter -> List Stringあとはこれらを Main でいい感じに呼び出すだけ.
おしまい
次回はいつになることやら.